Liigne, mis on. Mõiste tähendus

2024 Autor: Henry Conors | [email protected]. Viimati modifitseeritud: 2024-02-12 06:23

Artikkel kirjeldab statistika kui teaduse rolli. Vaadeldakse kurtoosi mõistet ja selle kasutamist teaduses.

Statistika. Põhikontseptsioon

Statistika on matemaatikateaduse põhituletis. See aine kuulub mitmetesse sotsiaalsetesse distsipliinidesse, mille eesmärk on kujundada õpilastes maailmapildist pilt ja asjatundlik analüüs sündmustest.

Statistika uurib igasuguseid protsesse ja sündmusi inimeste elus, toob esile nende mustrid ja esitab kõike lühikeste statistiliste aruannete kujul. Selline teadus on sotsiaalselt kasulik ja nõuab pidevat täiustamist. Liigne - mis see on? See on graafilise statistika põhikontseptsioon, mis aitab määrata täiusliku arvutuse õigsust. Kurtosis ei tohiks olla tugevat kõrvalekallet.

Statistika võimaldab teil rahuldada inimeste vajadust usaldusväärse teabe järele konkreetse nähtuse, sündmuse ja muu kohta. Elutegurite dünaamika, nende languse, paigalseisu või kasvu määramine – just seda see teadus teebki.

Kaasaegses maailmas on statistika teadusareenil üks peamisi kohti. Mõelgem mõistele "kurtosis". Mis on statistiline eesmärk ja vaatlus? Kus neid mõisteid rakendatakse? Loe selle kõige kohta lähem alt artiklistartikkel.

Mis on kurtosis statistikas?

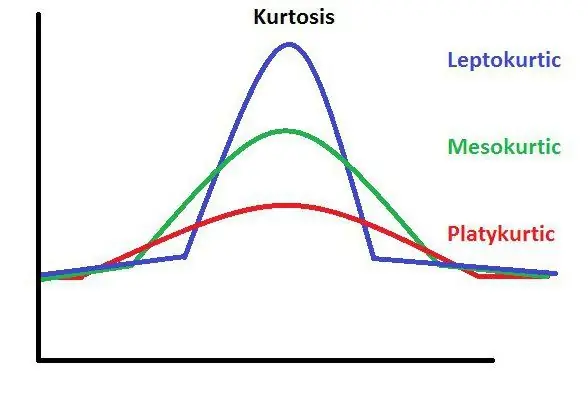
Kurtoos on statistiline mõiste, mis esindab jaotusgraafiku iga piigi teravust. Selle täpseks arvutamiseks on olemas spetsiaalne valem.

Oodatus väidab, et statistiliste andmete ühtlasemaks jaotamiseks peab kurtoos olema võrdne positiivse arvuga. Sõna otseses mõttes tähendab see mõiste teatud kõrvalekallet normist ja statistikasüsteemi edasist ebanormaalset arengut või toimimist.

Kortoosi liigne väljendus statistilisel graafikul võib viidata valele uuringule või vigadele graafiku algandmetes. Selline kontseptsioon on olemuselt skalaarne, mis tähendab, et lõpliku arvutuse tulemuseks peaks olema arv, mis ei sisalda muutujaid ega abifunktsioone. Selline näeb kurtosis välja.

Mis on sümmeetriline ja asümmeetriline jaotus

Kurtoos, mis on seotud sümmeetrilise tüübi jaotusega, võrdub nulliga. Seda saab graafikuga selgelt näidata. Asümmeetriline graafik näitab arvu, mis ei ole null. Nii tähistatakse kurtoosi.

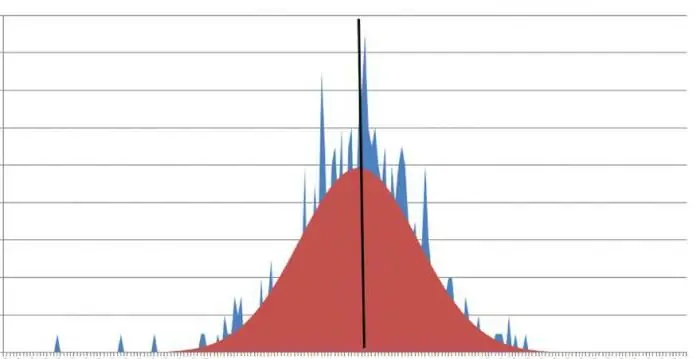
Mis on tipu teravus? Teravate tippudega graafik näitab, et kurtoosi väärtus on nullist väiksem arv. Tihti tuleb ette olukordi, kus antud mõistet ei saa väljendada eraldi väärtusega. Sel juhul läheneb see miinus- või plusslõpmatusele.